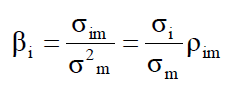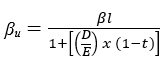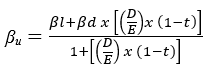Beta, seconda lettera dell’alfabeto greco, è utilizzata in finanza come coefficiente di rischio in diversi modelli teorici. Tuttavia, a prescindere dalle diverse configurazioni che può assumere, il suo significato è univoco: per definizione, beta rappresenta una misura del rischio sistematico di un’azienda, cioè quella parte di rischio non diversificabile e complementare al rischio specifico.
Matematicamente tale metrica è rappresentabile dalla seguente espressione:
dove
- βi= beta del titolo i;
- Ϭim= covarianza tra rendimento del titolo i e rendimento di mercato;
- Ϭ2m= varianza del rendimento del portafoglio di mercato;
- Ϭi= deviazione standard del rendimento del titolo i;
- Ϭm= deviazione standard del rendimento di mercato;
- ƿim= coefficiente di correlazione tra il rendimento del titolo e il rendimento di mercato.
Da qui, e più precisamente dal modello rischio-rendimento del Capital Asset Pricing Model, deriva l’interpretazione di beta. Il CAPM, di fatto, dimostra che per ogni titolo il rendimento atteso può essere calcolato come somma del rendimento dei titoli privi di rischio (come i titoli di stato) e un premio per il rischio a cui l’investitore si espone investendo in titoli rischiosi.
Il premio, a sua volta, è calcolato tenendo in considerazione quanto più è rischioso un determinato titolo rispetto all’indice di mercato, che per definizione è ben diversificato. È il beta ad assolvere a questa funzione, mettendo in relazione la volatilità dei rendimenti di un titolo con la volatilità dei rendimenti del mercato nella sua interezza.
In questa accezione, quindi, beta non è altro che la metrica usata per constatare se i rendimenti del titolo di un’azienda reagiscono in maniera più che proporzionale rispetto al movimento dei rendimenti di mercato, acquistando l’aggettivo di aggressivi (β>1), o viceversa in modo meno che proporzionale, guadagnandosi l’interesse degli investitori più prudenti e l’aggettivo di difensivi (β<1).
Tornando alla prima definizione data, il beta è uno degli elementi di maggior focus per gli analisti finanziari nel momento in cui si deve stimare il costo del capitale proprio di un’azienda. Per questo motivo, nonostante i modelli finanziari più utilizzati allo scopo varino nelle loro componenti, l’unico elemento costante in ognuno di essi è proprio beta. Più in dettaglio, è sempre presente il prodotto tra beta e la misura di rendimento marginale che un investitore richiede per impiegare il proprio capitale nel portafoglio di mercato piuttosto che in attività risk-free, il cosiddetto Equity Risk Premium.
Il calcolo di beta nei casi reali
Quando ci si imbatte nella misura di beta di un determinato titolo fornita da un particolare data service (Bloomberg, T. Reuters e altri), questa deriva generalmente da una regressione lineare dei rendimenti del titolo sui rendimenti dell’indice di mercato preso come riferimento. Tuttavia non sempre è così facile ottenere questa informazione, soprattutto nel caso in cui si ha a che fare con titoli non liquidi (cioè con bassi volumi di negoziazione) o peggio con aziende private non quotate in borsa.
Nel primo caso, infatti, si potrebbe giungere all’ingenua conclusione che certi titoli abbiano beta relativamente bassi quando in realtà ciò è dovuto ai loro rendimenti, i quali si muovono con ritardo rispetto a quelli del mercato a causa dei bassi volumi di negoziazione. In questa situazione il valore di beta perde totalmente di significatività, dato che dipende esclusivamente dall’assenza, o quasi, di variazione nei rendimenti del titolo.
Nel secondo caso, invece, il problema è sostanziale, non essendo disponibili dati sui rendimenti dei titoli di società private, e quindi essendo impossibile impostare qualsiasi tipo di regressione.
In entrambi i casi citati si dovrà allora stimare il valore di beta utilizzando il corrispettivo parametro di aziende simili che abbiano azioni quotate e sufficientemente liquide. In pratica si seleziona un pool di aziende ritenute comparabili in termini di grandezza, di performance e business model adottato. Si passa poi al calcolo dei beta di queste e al successivo deleverage, cioè il processo di depurazione dei singoli beta dall’effetto leva finanziaria, la quale può variare anche di molto nei diversi casi.
Lo step finale consiste nel calcolare la media (o la mediana) dei beta unlevered ottenuti e poi aggiungere al beta medio (mediano) risultante il livello di leverage caratteristico dell’azienda oggetto di valutazione. Per effettuare tale procedura si utilizza la formula di Hamada o, nel caso il debito sia considerato rischioso (βd>0) la formula di Fernandez, riportate di seguito.
Formula di Hamada
dove
- βu= beta unlevered dell’azienda comparabile i;
- βl= beta levered dell’azienda comparabile i;
- D/Ec = rapporto debt/equity dell’azienda comparabile i;
- t= tax rate marginale.
Formula di Fernandez
- βu= beta unlevered dell’azienda comparabile i;
- βl= beta levered dell’azienda comparabile i;
- βd=beta del debito dell’azienda comparabile i;
- D/Ec = rapporto debt/equity dell’azienda comparabile i;
- t= tax rate marginale.
Come si può evincere dalle due espressioni, a numeratore viene posto il beta levered i, cioè quello ottenuto per ogni azienda comparabile attraverso la regressione. Questo sarà infatti espressione del rischio di ogni specifica azienda comparabile, compreso quello generato dal livello di leverage finanziario. Tuttavia il livello di leva finanziaria è diverso per ogni impresa, inclusa quella per cui si vuole stimare beta, quindi a denominatore si pone un fattore depurativo del beta levered, dato dallo specifico livello di leverage dell’azienda comparabile al netto dell’effetto fiscale.
Si capisce quindi quanto queste procedure siano esposte alla soggettività di chi le applica, e quanto questo possa avere un impatto rilevante sul costo del capitale proprio ottenuto nei passaggi successivi. È allora di fondamentale importanza l’esperienza dell’analista nell’applicare i necessari aggiustamenti e le giuste accortezze per ottenere una stima di beta il più ragionevole possibile.