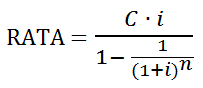L’assunzione di un debito determina la necessità di stabilire le modalità attraverso le quali procedere alla relativa estinzione. Per questo motivo esistono i piani di ammortamento. Riprendendo la definizione presentata da Ubi Banca:
<<Il piano di ammortamento rappresenta il piano dettagliato della restituzione del capitale prestato più gli interessi maturati dalla banca. In esso viene stabilito l’importo, la data entro la quale tutto il debito deve essere pagato, la periodicità di ciascuna rata (mese, trimestre, semestre), i criteri per determinare l’ammontare di ogni rata e il debito residuo. Le rate di un piano di ammortamento sono composte da due elementi principali: la quota capitale e la quota di interesse.>>
Mentre la quota capitale è costituita dall’ammontare preso a prestito, la quota interessi rappresenta il ritorno economico del soggetto finanziatore, di solito l’istituto bancario.
Diversi tipi di piani di ammortamento
Il modello francese
La tipologia più diffusa è la versione francese, conosciuta anche come ammortamento a rate costanti. Essa prevede rate posticipate, tutte che prevedono lo stesso versamento, ciascuna comprendente una quota capitale ed una quota interessi.
Il metodo per il calcolo della rata consiste nell’applicazione della seguente formula:
Dove “C” è il capitale, “i” il tasso d’interesse ed “n” il numero di rate da rimborsare.
Per semplicità, si suppone che si sia preso in prestito un capitale di €20.000, al tasso del 5% annuo, da restituire in 10 rate semestrali.
Il risultato, secondo il modello francese, sarebbe il seguente:
| Semestre | Rata | Quota interessi | Quota capitale | Capitale residuo |
| 1 | 2285.18 | 500 | 1785.18 | 18214.82 |
| 2 | 2285.18 | 455.37 | 1829.81 | 16385.01 |
| 3 | 2285.18 | 409.63 | 1875.55 | 14509.46 |
| 4 | 2285.18 | 362.74 | 1922.44 | 12587.02 |
| 5 | 2285.18 | 314.68 | 1970.50 | 10616.52 |
| 6 | 2285.18 | 265.41 | 2019.77 | 8596.75 |
| 7 | 2285.18 | 214.92 | 2070.26 | 6526.49 |
| 8 | 2285.18 | 163.16 | 2122.02 | 4404.47 |
| 9 | 2285.18 | 110.11 | 2175.07 | 2229.40 |
| 10 | 2285.18 | 55.74 | 2229.40 | 0.00 |
| Totale | 22851.80 | 2851.80 | 20.000 |
Come si può notare, la rata è costante (€2285.18) ed a variare sono la quota capitale (crescente) e la quota interessi (decrescente). Si evince come si paghino quasi €3000 di interessi su un capitale ottenuto di €20.000 (essi sono stati calcolati applicando i 6/12 del 5% al capitale residuo, ossia il 2,5%).
Il modello italiano
Passando alla versione nostrana, il piano d’ammortamento italiano, come quello francese, è caratterizzato dalla costanza delle rate, individuabile in questa circostanza nella quota capitale (C/n). Gli interessi, come al solito, sono determinati avendo come benchmark il capitale residuo.
Con un prestito di €20.000 ed un tasso d’interesse del 5% darestituire in 10 rate, nel modello italiano si osservano questi risultati:
| Semestre | Rata | Quota interessi | Quota capitale | Capitale residuo |
| 1 | 2500 | 500 | 2000 | 18000 |
| 2 | 2450 | 450 | 2000 | 16000 |
| 3 | 2400 | 400 | 2000 | 14000 |
| 4 | 2350 | 350 | 2000 | 12000 |
| 5 | 2300 | 300 | 2000 | 10000 |
| 6 | 2250 | 250 | 2000 | 8000 |
| 7 | 2200 | 200 | 2000 | 6000 |
| 8 | 2150 | 150 | 2000 | 4000 |
| 9 | 2100 | 100 | 2000 | 2000 |
| 10 | 2050 | 50 | 2000 | 0 |
| Totale | 22.750 | 2750 | 20.000 |
La quota capitale è costante (€2000) mentre variano gli interessi (decrescenti) e la rata (decrescente). E’ chiaro come gli interessi pagati si riducano.
Il modello tedesco
Infine, la metodologia tedesca è anch’essa molto simile a quella francese ma si distingue per un particolare, ossia gli interessi sono corrisposti in via anticipata. Per essere più precisi, la prima rata si compone per intero di interessi mentre l’ultima solo di capitale. Quelle intermedie, invece, hanno una quota di interessi ed una di capitale. Di solito, la rata rimane costante mentre variano le altre due componenti. Il calcolo avviene secondo la seguente espressione:
Rata = C / ((1+TA/PA) / TA/PA) x (1 – (1 / (1 + TA/PA)(PA x A)))
Dove “C” è l’importo del finanziamento, “TA” il tasso annuo del finanziamento espresso in decimali, “PA” il numero di rate pagate nel corso dell’anno, “A” il numero di anni previsti complessivamente per il rimborso. La prima rata, di soli interessi, sarà naturalmente diversa dalle altre e sarà calcolata secondo la seguente equazione:
1° rata = (C x TP) / (1 + TP)
Dove TP è il tasso di interesse del periodo.