
Harry Markowitz è considerato uno dei maggiori pionieri dell’economia contemporanea. Ha ricevuto il premio Nobel nel 1990 per il saggio pubblicato nel 1959 Portfolio Selection: Efficient Diversification, in cui espone la sua Modern Portfolio Theory. La teoria sarà stata poi approfondita, dal punto di vista formale, da William Sharpe, altro premio Nobel, conosciuto per il modello matematico Capital Asset Pricing Model. Esso è tutt’ora uno degli strumenti più usati per l’analisi dei prezzi nel mercato.
Prima della Modern Portfolio Theory, che fornisce un modello d’investimento matematico statistico, gli investitori adottavano tecniche empiriche basate in gran parte sull’intuizione per valutare il rischio ed il rendimento delle diverse operazioni. Inoltre, l’analisi era condotta titolo per titolo e non sull’interno portafoglio, come invece presuppone la Modern Portfolio Theory. Secondo gli studi di Markowitz, infatti, la combinazione stessa dei titoli deve presentare un adeguato rapporto rischio-rendimento per poter essere considerata vantaggiosa per l’investitore.
Principi fondamentali e il modello
Gli assunti fondamentali della Modern Portfolio Theory sono:
- Gli investitori sono razionali ed avversi al rischio, desiderano massimizzare la ricchezza finale (valore atteso) e minimizzare il rischio, espresso dalla deviazione standard;
- Il mercato è perfettamente concorrenziale e l’asimmetria informativa è assente;
- I costi di transazione e le imposte sono trascurabili, gli investitori inoltre hanno accesso illimitato al capitale, cioè possono prendere in prestito denaro a un tasso d’interesse privo di rischio (risk-free rate);
- Si considera un unico periodo di investimento valido per tutti i partecipanti al mercato.
Il modello di Markowitz formalizza questi principi attraverso l’analisi statistica. I profitti vengono considerati come delle variabili casuali continue, cioè che dipendono da un fenomeno aleatorio e che possono assumere valori diversi in base all’evolversi dei fattori da cui dipendono. Di queste variabili si possono analizzare i valori attesi, la deviazione standard e la correlazione.
La distribuzione delle variabili nella Modern Portfolio Theory è rappresentata dalla Curva Normale Gaussiana, il cui punto più alto corrisponde al valore medio atteso dei dati osservati, ovvero quello più probabile.
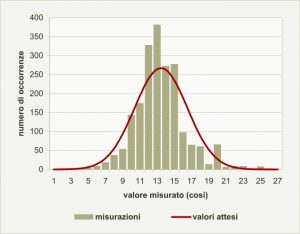
Gli studi di Markowitz dimostrano che, attraverso un’oculata scelta dei titoli, il portafoglio da essi composto presenta un rischio minore rispetto alla media ponderata dei singoli titoli considerati individualmente o per classe di rischio. Dai possibili portafogli (feasible portfolios) risultanti dall’analisi, è possibile identificare i portafogli efficienti (efficient portfolios). L’algoritmo utilizzato per generare la curva è conosciuto come Mean Variance Optimization.
Diversificazione
I risultati ottenuti dalla Modern Portfolio Theory poggiano sul concetto di diversificazione finanziaria, che consiste nella riduzione della rischiosità del rendimento di un portafoglio di titoli grazie all’utilizzo di più strumenti finanziari i cui rendimenti non sono perfettamente correlati. La correlazione tra i vari strumenti finanziari si determina in campo statistico attraverso l’indice di Pearson, o coefficiente di correlazione.
L’indice di Pearson esprime un’eventuale relazione lineare tra variabili ed il suo valore è compreso tra -1 e 1.
- se la correlazione > 0, i titoli sono positivamente correlati;
- se la correlazione < 0, i titoli sono negativamente correlati;
- se la correlazione = 0, i sono non sono correlati.
Quando la correlazione è inferiore all’unità, ossia è imperfetta, la diversificazione dei titoli del portafoglio è in grado di minimizzare il rischio. Quindi, meno i titoli sono correlati e più il portafoglio è efficiente.
Modelli alternativi
Successivamente alla Modern Portfolio Theory sono stati proposti diversi modelli statistici che invece giungono a distribuzioni asimmetriche per descrivere il rischio. Tutte le proposte nate come osservazioni o critiche alla teoria di Markowitz compongono quella che è chiamata Post Modern Portfolio Theory.




