
Dal lavoro pionieristico di Louis Jean Baptist Bachelier, La Teoria della Speculazione del 1900, la finanza moderna iniziò a prendere forma. Dopo lo studio del matematico francese in economia si iniziò a prendere come modello un noto fenomeno fisico, il moto browniano, per analizzare l’evoluzione dei prezzi sui mercati azionari.
Descrizione del moto browniano
Grazie all’invenzione del microscopio è stato possibile osservare per la prima volta i movimenti caotici dei granelli di polline sulla superficie dell’acqua. Un botanico scozzese, Robert Brown, agli inizi dell’800 studiò questi movimenti, senza però riuscire a spiegarli. Per questo, il comportamento delle particelle in condizioni simili al polline sull’acqua venne chiamato moto browniano.
Nel 1905 Albert Einstein diede una spiegazione fisica al fenomeno attribuendo la causa del movimento irregolare delle particelle di polline allo scontro ripetuto con le microscopiche molecole d’acqua soggette a moti termici casuali. Einstein contribuì alla causa non solo concettualmente ma anche con una descrizione quantitativa del fenomeno, aprendo le porte allo studio del cosiddetto random walk.
Prima applicazione in ambito finanziario
Quando Einstein elaborò le equazioni per il moto browniano non sapeva che un modello matematico simile era già stato elaborato da un giovane matematico e dottorando francese di nome Louis Bachelier. Egli però non era interessato al movimento delle particelle di polline quanto piuttosto ai movimenti altrettanto caotici della Borsa di Parigi.
La tesi di Bachelier dal titolo Théorie de la Spéculation aveva l’obiettivo di sviluppare delle formule per determinare il prezzo di complessi strumenti derivati. Per fare ciò era necessario capire come variano i prezzi delle azioni alla base di tali strumenti. L’autore specificò nell’introduzione della sua ricerca che
«la determinazione di queste attività dipende da un numero infinito di fattori: dunque non si può assolutamente sperare di poter formulare una previsione matematica (esatta)».
L’idea fondamentale di Bachelier
Il giovane matematico cercò di stimare la probabilità della variazione dei prezzi ed iniziò considerando il mercato delle obbligazioni come un gioco equilibrato. Per comprendere tale concetto si può immaginare un possibile gioco tra un croupier ed un giocatore. Il croupier lancia una moneta non truccata per N volte. Quando compare testa, il giocatore vince 1 euro, viceversa, quando compare croce perde 1 euro. Ad ogni lancio sia testa che croce hanno la stessa possibilità di presentarsi. Ogni lancio è quindi indipendente da quello precedente, ovvero il fatto che sia uscito testa la prima volta non implica che al secondo lancio si presenti di nuovo testa.
In parole semplici, l’idea principale di Bachelier è che la moneta, dal punto di vista probabilistico, dopo una lunga serie di lanci dovrebbe portare un profitto pari a zero.
Random Walk
Nell’esperimento mentale del gioco equilibrato con la moneta si tiene traccia del risultato (+1,-1) per ogni lancio. Questo realizza ciò che in matematica viene definito un processo stocastico o aleatorio, detto anche random walk, ovvero passeggiata casuale. Questo termine fu introdotto per la prima volta nel 1905 dallo statistico Karl Pearson, che illustrò il problema utilizzando la metafora dell’uomo ubriaco che cammina barcollando in un campo aperto. L’uomo, barcollante, durante il suo percorso farà qualche passo in una direzione, poi in un’altra e così via. Trascorso un po’ tempo, se si volesse cercare l’uomo ubriaco dove si dovrebbe guardare? Il posto più probabile dove trovare l’uomo è proprio nelle vicinanze del suo punto di partenza.
Alla stregua della moneta, questo esperimento mentale può descrivere il cammino casuale di una particella che si può muovere in ogni direzione con la stessa probabilità. Allo stesso modo, può descrivere le fluttuazioni del prezzo delle azioni, il quale compie una serie di movimenti aleatori. Il prezzo può salire o scendere ma in media oscillerà intorno al punto di partenza. Bachelier partì proprio da questi fondamentali concetti per la costruzione del suo modello.
Limiti del pensiero di Bachelier
La rivoluzionaria teoria di Bachelier ha anche diversi limiti. Infatti, usando il random walk per descrivere il percorso del prezzo di un titolo è possibile, per la natura stessa del processo, che questo superi la soglia dello zero, generando così numeri negativi per i prezzi, cosa che nel mondo reale non può accadere. Dopo che l’economista Paul Samuelson nel 1960 ha riscoperto il lavoro del matematico francese, la teoria di Bachelier è stata rivista supponendo che ad interessare non è tanto la variazione del prezzo, ma la variazione proporzionale del prezzo. Questo problema, matematicamente, può essere gestito con il logaritmo.
Oltre al fatto che i prezzi non si muovono di una sola unità, un’ulteriore differenza fra il modello di Bachelier e la finanza reale è che i mercati si muovono in tempo continuo. Il tempo spazia sull’intera linea dei numeri reali positivi, e non in tempo discreto dove invece esso assume valore nell’insieme dei numeri naturali (t=0, 1, 2, 3, e così via), come nell’esempio della moneta. A tal proposito, Bachelier ideò un’importante teoria per il passaggio dal discreto al continuo, purtroppo non rendendola mai rigorosa per mancanza degli strumenti matematici necessari.
Il punto di vista matematico
Nel 1923 Norbert Wiener produsse una costruzione matematica rigorosa della teoria di Bachelier, direttamente nel tempo continuo, basata sul processo del moto browniano. Infatti, matematicamente, un moto browniano è descritto da quello che è detto processo di Wiener , che è un processo stocastico indicizzato da tempo continuo. In questo caso si inizia da un tempo uguale a zero.
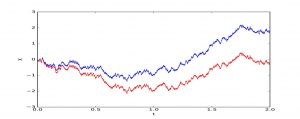
Il moto browniano possiede alcune proprietà rilevanti. Gli incrementi descritti nel processo di Wiener, per esempio, sono indipendenti e si distribuiscono normalmente. La distribuzione di probabilità, in statistica, è una funzione che mostra i possibili valori per una variabile e quanto spesso essi si verificano. La distribuzione più famosa ed utilizzata è appunto la distribuzione normale, espressa dalla curva di Gauss, usata per spiegare tanti fenomeni naturali ed economici. Se i valori seguono questa curva, che prende la forma di una campana, nella pratica non si troverà quasi mai un caso che si discosta molto dalla media. Questa distribuzione di probabilità può descrivere variabili come l’altezza di una popolazione, i punteggi del test del QI o, tornando a Bachelier, i guadagni giocando a testa o croce.
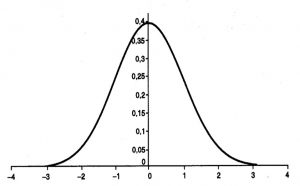
Come intuì Bachelier, se si dispongono in un diagramma tutte le variazioni di prezzo di un’obbligazione relative ad un determinato periodo di tempo, queste si dispongono nella consueta forma di una curva a campana.
Precursore di idee rivoluzionarie
Nel 1965, il dottorando all’università di Chicago Eugene Fama prendendo spunto dalle considerazioni di Bachelier formulò la cosiddetta Ipotesi del Mercato efficiente, fornendo così la base su cui poggia la teoria finanziaria moderna. Secondo Bachelier, le fluttuazioni dei prezzi erano causate per la maggior parte da fattori irrazionali, che nell’insieme si annullano simmetricamente generando aspettative di profitto pari a zero. Fama piuttosto attribuì la casualità ai Mercati efficienti, in cui la concorrenza tra partecipanti del tutto razionali conduce ad una situazione in cui i prezzi dei singoli titoli, in qualsiasi momento nel tempo, riflettono già gli effetti delle informazioni di eventi accaduti e che dovranno accadere.
In un Mercato efficiente, in qualsiasi momento, il prezzo effettivo del titolo sarà una stima del suo valore intrinseco. La versione di Fama non si discosta dal risultato della passeggiata casuale di Bachelier, ma ne deduce una caratteristica più avvincente: i mercati sono impossibili da prevedere non perché irrazionali ma perché già incorporano tutte le informazioni disponibili.



